We use the integral form of Faraday's Law,
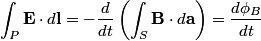 If we take the path 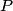 to be the circular wire loop (and we neglect the fact that it appears not to be a complete circle in the figure), then the left-hand side of the equation above is equal to the induced emf. to be the circular wire loop (and we neglect the fact that it appears not to be a complete circle in the figure), then the left-hand side of the equation above is equal to the induced emf.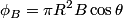 where 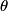 is the angle between the normal to the circular loop and the magnetic field. The wire loop rotates with an angular speed of is the angle between the normal to the circular loop and the magnetic field. The wire loop rotates with an angular speed of  , therefore, , therefore, 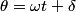 where where 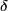 is a constant. is a constant.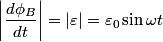 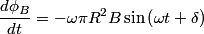 So, 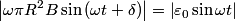 This equation can only hold if 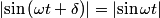 It follows then that 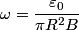 Therefore, answer (C) is correct. |